10814. Disjoint Sets Union 2
Implement disjoint sets union data
structure. You have to perform queries of two types:
·
union
u v – unite two
sets that contain u and v, respectively;
·
get
v – find the
set to which v belongs to, find the minimal and the maximal element of
the set, and the total number of elements in it.
Input. The first line contains two integers n and m
(1 ≤ n, m ≤ 3 * 105) – the number of
elements and the number of queries. Next m lines contain queries, one
per line.
For a query union the line
looks like union u v (1 ≤ u, v ≤ n).
For a query get the line
looks like get v (1 ≤ v ≤ n).
Output. For each operation get you should output the result
on a separate line in the respected order. Each result should consist of three
integers: the minimal element, the maximal element, and the number of elements
in the set.
|
Sample
input |
Sample
output |
|
5 11 union 1 2 get 3 get 2 union 2 3 get 2 union 1 3 get 5 union 4 5 get 5 union 4 1 get 5 |
3 3 1 1 2 2 1 3 3 5 5 1 4 5 2 1 5 5 |
SOLUTION
disjoint sets union
Algorithm analysis
Implement a disjoint sets union data structure with heuristics.
In the union
operation make the recalculation
of the minimum and maximum elements of a set, as well as the number of its
elements.
Initially, we
have n sets of one element, the i-th set
contains only one number i. The minimum amin[i] and the maximum amax[i]
in the i-th set are initially equal to i. The size of the i-th
set cnt[i] is 1.
Let
a set with a representative y be added to a set with a representative x.
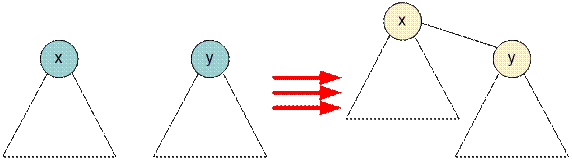
Then the minimum, maximum and number of elements in the set
are recalculated as follows:
·
cnt[x] = cnt[x] + cnt[y];
·
amin[x] = min(amin[x], amin[y]);
·
amax[x] = max(amax[x], amax[y]);
Example
Let’s
simulate the queries from the sample.
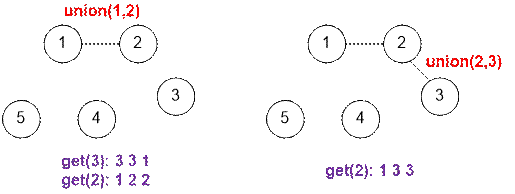
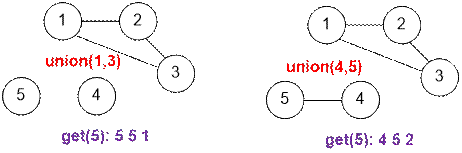
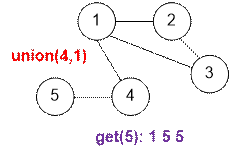
Algorithm realization
Declare
the arrays:
·
parent – array of parents for DSU;
·
depth – contains the height of the tree, used for heuristics;
·
amin, amax – arrays keep minimum and maximum elements in sets;
·
cnt
– an array to hold the number of elements in sets;
#define MAX 300001
int parent[MAX], depth[MAX],
amin[MAX], amax[MAX], cnt[MAX];
Function Repr finds
a representative of the set that contains vertex v.
int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
Function Union unites
sets that contain vertices x and y.
void Union(int x, int y)
{
Find
the representatives of x and y.
x = Repr(x), y = Repr(y);
if (x == y) return;
Implement
the tree height heuristic. The set with a lower height is attached to a set with
a higher height.
if (depth[x] < depth[y]) swap(x, y);
parent[y] = x;
if (depth[x] == depth[y]) depth[x]++;
The
number of vertices from the set with element y is added to the set where
x is located.
cnt[x] += cnt[y];
Recalculate
the minimum and maximum elements in the sets.
if (amin[y] < amin[x]) amin[x] = amin[y];
if (amax[y] > amax[x]) amax[x] = amax[y];
}
The
main part of the program. Read the input data. Initialize the arrays.
Initially, we have n sets of one element. The minimum and maximum in the
i-th set equals to i. The size of the i-th set cnt[i]
is 1.
The
height of each set depth[i] is initially assumed to be 0.
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++) parent[i] = i;
for (i = 1; i <= n; i++) amin[i] = amax[i] = i;
for (i = 1; i <= n; i++) cnt[i] = 1;
Process
m queries sequentially.
for (i = 0; i < m; i++)
{
scanf("\n");
scanf("%s %d", s, &u);
if (s[0] == 'u')
{
scanf("%d", &v);
Union
the sets that contains elements u and v.
Union(u, v);
}
else
{
Find
a representative of the set containing element u.
int u1 = Repr(u);
Print the minimum and maximum
element of the set, as well as the number of its elements.
printf("%d %d
%d\n", amin[u1], amax[u1],
cnt[u1]);
}
}